Hay dos casos:
En la resta de fracciones nos podemos encontrar dos casos diferentes:
- Fracciones que tienen el mismo denominador
- Fracciones
que tienen el distinto denominador
Primer caso: fracciones que tiene el mismo denominador.
La resta de dos ó más fracciones que tienen el mismo denominador es muy sencilla, sólo hay que restar los numeradores y se deja el denominador común.
Ejemplo:
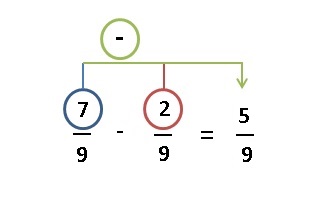
Segundo caso: fracciones con diferente denominador.
La resta de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso
1. Multiplicar en cruz. Se multiplica el numerador de la primera fraccion por el denominador de la segunda, y el denominador de la primera por el numerador de la segunda. Ambas multiplicaciones se restan.
Ejemplo:
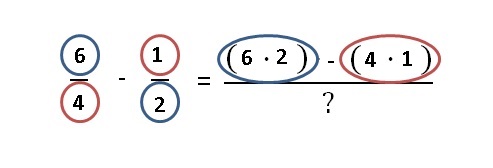
2. Multiplicar los denominadores de las dos fracciones. Se multiplican los denominadores de las dos fracciones.
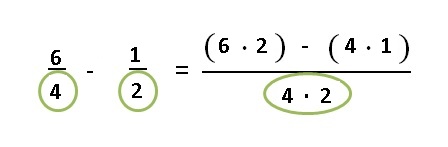
3. Resolvemos todas las operaciones.
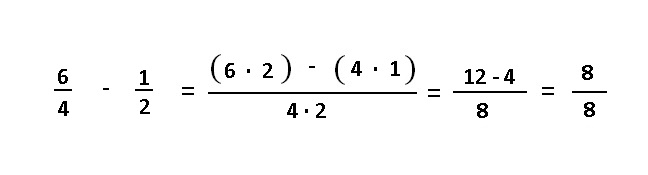
Observamos que 8 es multiplo de 2. Por lo que dividimos el 8 del denominador y del numerador por este número.
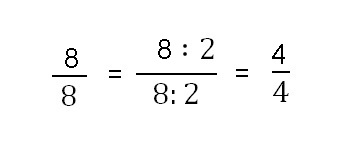
Otra forma de hacerlo:
La resta de dos o más fracciones con distinto denominador es un poco menos sencilla. Vamos paso a paso:
1º Se haya el mínimo común múltiplo de los dos denominadores
2º Se calcula el numerador con la fórmula: numerador antiguo x denominador común y dividido por denominador antiguo
3º Se procede como en el primer caso (dado que las fracciones tienen el mismo denominador)
Ejemplo:
6/4 - 1/2
1º Calculamos el mínimo común múltiplo (m. c. m.) el m.c.m. (4, 2) = 4.
2º Calculamos los
numeradores.
Numerador de la primera fracción: 6 x
4 : 4 = 6
Numerador de la segunda fracción: 1 x 4 : 2 = 2
3º
Tenemos pues una fracción que es:
6/4 - 2/4
Como
los denominadores son idénticos podemos restarla como en el caso 1
4º Resta
| 6 | 2 | 4 | ||
| ------- | - | ------ | = | ----- |
| 4 | 4 | 4 |
Vídeo explicativo:
Reglas divisibilidad |
Máximo Común Divisor (M. C. D.) |
Más apuntes de matemáticas |
|
