El mínimo común múltiplo (m. c. m.) de dos o más números es el menor múltiplo común distinto de cero.
Para hallar el mínimo común múltiplo de dos o más números debemos de descomponer el número en factores primos.
Por ejemplo:
Buscaremos en mínmo común multiplo de 40 y 60.
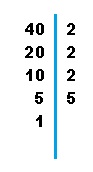
1. Descomponemos en factores primos el 40:
|
En este paso hemos dividido 40:2=20. Ahora buscaremos el mínimo divisor de 20 que es 2 y hacemos lo mismo 20:2= 10. Y seguiremos haciendo lo mismo con todos los anteriores. |
Por lo tando 40 se descompone en:
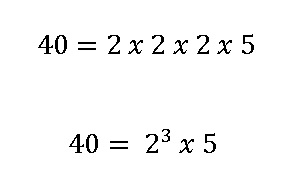
2. Una vez descompuesto el 40, haremos lo mismo con el 60.
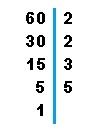
Por lo tanto 60 se descompone en:
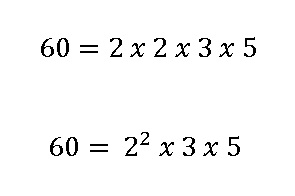
3. Para hallar el mínimo común divisor (mcd) de 40 y 60, para ello, tenemos que coger los comunes y no comunes al mayor exponente.
Por lo que se quedaria:
mcm (40 y 60)= 2 x 2 x 2 x 3 x 5 = 120
Por lo que el mínimo común multiplo de 40 y 60 sería 120.
¡Truco! Si quieres saber si has hecho bien la descomposición de factores primos se puede comprobar multiplicando. Empezando por abajo, multiplicas el último número de la izquierda (multiplicando) con el último de la derecha (multiplicador), el resultado debe ser el número de arriba del multiplicando
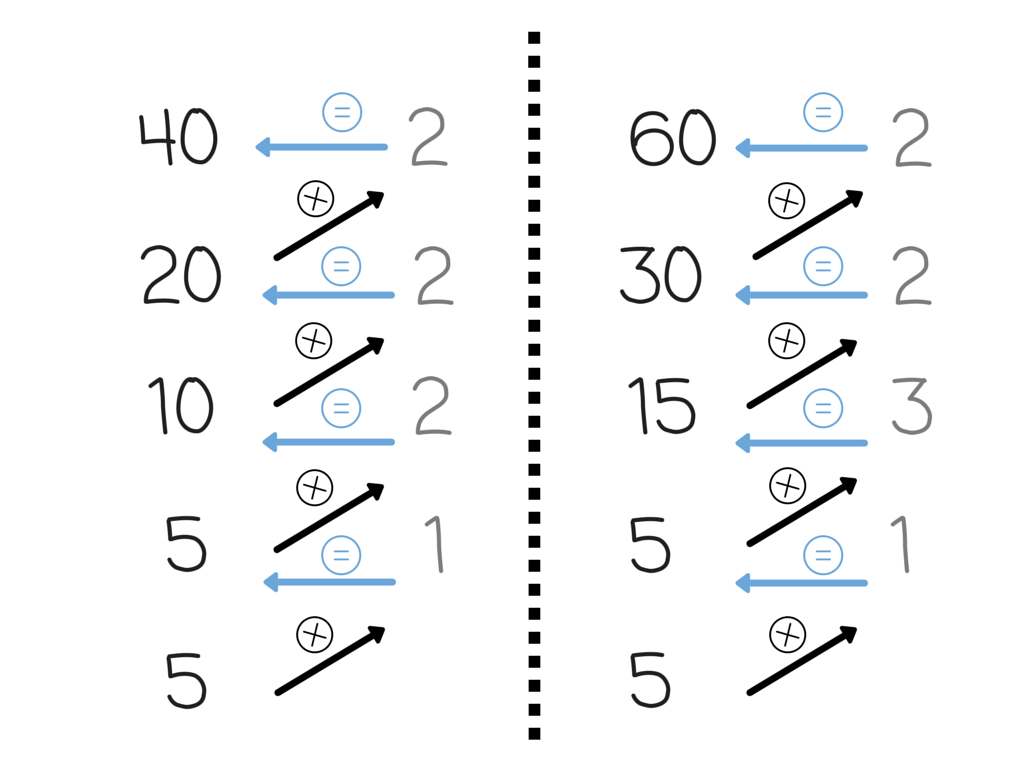 |
El último número es el 5 (multiplicando) el multiplicador será el 1 y el resultado es el 5. Lo mismo pasa si 5 (multiplicando) lo multiplicas por 2 (multiplicador) es igual a 10. |
Otros ejemplos del mínimo común múltiplo (mcm)
Ejemplo: Averiguar el m.c.m. de Sacar el M.C.D. de 20 y 10:
20 = 20, 40, 60, 80.....
10= 10, 20, 30, 40....
20 es el múltiplo menor que es común a ambos números.
Múltiplos: los múltiplos de un número se obtienen multiplicando dicho número por los números naturales 0, 1, 2, 3, 4, 5.....
Ejemplo:
múltiplos del 7:
7x0 = 0; 7x1 = 7;
7x2 = 14; 7x3 = 21;
7x4 = 28; 7x5 = 35 ....
O sea son múltiplos del 7: 0,
7, 14, 21, 28, 35, 42, 48, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133,
140, 147, 154, 161, 168...
Ejemplo: Calcular el m. c. m. de 4, 5 y 6.
Se hace la descomposición de factores (que ya la explicamos en el máximo común divisor). Lo hacemos de la siguiente forma:
4= 2x2
5= 5
6= 2x3
Se toman los factores comunes y no comunes con el mayor exponente y se multiplican: 2x2 x3 x5 = 60. El mcm de 4, 5 y 6 es 60.
Problemas de ángulos |
Geometría Conceptos Generales |
Más apuntes de matemáticas |
|